
آخرین ویدیو ها در آپارات
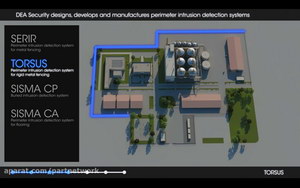 |
| حفاظت پیرامونی DEA ایتالیا (PIDS) . کمپانی DEA Security یکی از تولیدکنندگان برجسته در حفاظت پیرامونی دنیاست که از دهه هشتاد در حوزه حفاظت پیرامونی فعال بوده است. این کمپانی از ابتدای قرن بیست و یکم وارد حوزه تولیدکنندگان برند در زمینه حفاظت پیرامونی شده است. کمپانی DEA با تولید طیف وسیعی از محصولات حفاظت پیرامونی و حفاظت الکترونیک توانسته جایگاه مناسبی در اروپا و ایتالیا در این حوزه بدست بیاورد. در فیلم پیش رو به معرفی این کمپانی میپردازیم. |
 |
| دوربینهای Ultra-HD برند اسپارک. فیلم تبلیغاتی کمپانی اسپارک ایتالیا از تجهیزات ویژه در حوزه Ultra HD - برند اسپارک ایتالیا با حوزه تخصصی در زمینه دوربینهای مداربسته Ultra-HD و 4K دارای تولیداتی برای مصارف ویژه است. فضاهای وسیعی که با دوربینهای نظارت تصویریمعمولی قابل پوشش نیست و موقعیتهائی که در آنها نیاز به کیفیت بسیار بالاتر از حد معمول وجود دارد. |
 |
| برند هلوکیبل آلمان پیشتاز کابلهای شبکه و فیبر نوری دنیا. برند هلوکیبل توانسته یک به یک پله های ترقی را طی نموده و در میان برندهای برتر حوزه شبکه و زیرساخت جهان قرار بگیرد. هلوکیبل با تولید کامل کالاهای خود در اروپا و استانداردهای اروپائی قابلیت این را دارد تا با شرایط مناسبی در کلیه پروژه های صنعتی و نفتی حضور داشته باشد. در فیلم بحث تولیدات این شرکت را در آلمان مشاهده مینمائید. |
ویدیو های دیگر... |
























